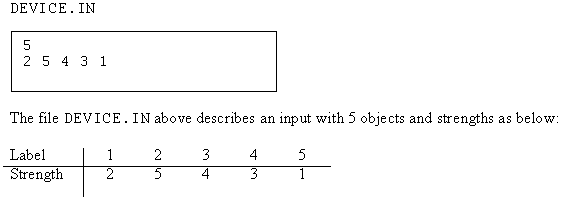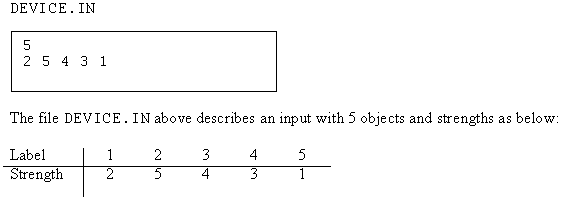PROBLEM
A
new space experiment involves N objects, labeled from 1 to N. It is known
that N is odd. Each object has a distinct but unknown strength expressed
by a natural number. For each strength Y, it holds that 1<=Y<=N. The
object with median strength is the object X such that there are equally
many objects having smaller strength than X as there are objects having
greater strength than X. You are to write a program that determines the
object with median strength. Unfortunately, the only way to compare the
strengths is by a device that, given three distinct objects, determines the
object with median strength among the three objects. LIBRARY
You are given a library named device with three
operations:
- GetN, to be called once at the beginning without arguments; it
returns the value of N.
- Med3, called with three distinct object labels as arguments; it
returns the label of the object with median (middle) strength.
- Answer, to be called once at the end, with one object label as
argument; it reports the label of object X with median strength and properly
ends the execution of your program.
The library device produces two
text files: MEDIAN.OUT and MEDIAN.LOG. The first line of file MEDIAN.OUT
contains one integer: the label of the object passed to the library in the call
to Answer. The second line will contain one integer: the number of calls to Med3
that have been performed by your program. The dialogue between your program and
the library is recorded in the file MEDIAN.LOG.
Instruction for Pascal programmers: Include the import
statement
uses device;
in the source code.
Instructions for C/C++ programmers: Use the
instruction
#include "device.h" in the source code, create a project
MEDIAN.PRJ and add the files MEDIAN.C (MEDIAN.CPP) and DEVICE.OBJ into this
project.
EXPERIMENTATION
You can experiment with the
library by creating a text file DEVICE.IN. The file must contain two
lines. The first line must contain one integer: the number of objects N. The
second line must contain the integers from 1 to N in some order: the ith integer
is the strength of the object with label i.
EXAMPLE
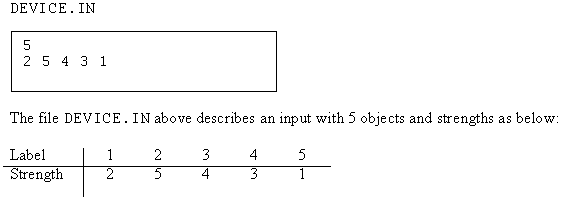
Here is a
correct sequence of 5 library calls:
1. GetN (in Pascal) or GetN() (in C/C++)
returns 5.
2. Med3(1,2,3) returns 3.
3. Med3(3,4,1) returns 4.
4.
Med3(4,2,5) returns 4.
5. Answer(4)
CONSTRAINTS
- For the number of objects N we have 5<=N<=1499 and N
is odd.
- For the object labels i, we have 1<=i<=N.
- For the object strengths Y, we have 1<=Y<=N and all strengths
are distinct.
- Pascal library file name: device.tpu
- Pascal function and procedure declarations:
- function GetN: integer;
- function Med3(x,y,z:integer):integer;
- procedure Answer(m:integer);
- C/C++ library file names: device.h, device.obj (use large memory model)
- C/C++ function headers:
- int GetN(void);
- int Med3(int x, int y, int z);
- void Answer(int m);
- No more than 7777 calls of function Med3 are allowed per run.
- Your program must not read or write any files.
Download File zip