For mange år siden mødtes Kong Arthur og hans Riddere om det Runde Bord hver Nytårsdag for at fejre deres fællesskab.
Til minde om disse begivenheder vil vi betragte et brætspil for én spiller, hvor én konge og et antal riddere placeres tilfældigt på hvert sit felt.
Brættet består af 8´8 kvadratiske felter.

Figur 1. Et bræt
Kongen kan flyttes til ethvert nabofelt, fra l til ¡ som vist på figur 2, forudsat selvfølgelig at den ikke flyttes ud over brættets kant.
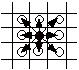
Figur 2. Alle kongens mulige bevægelser
En ridder (den brik kaldes normalt på dansk for en springer) kan flyttes fra l til ¡ som vist på figur 3, forudsat selvfølgelig at den ikke flyttes ud over brættets kant.
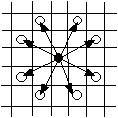
Figur 3. Alle ridderens mulige bevægelser
Under spillet kan spilleren placere mere end én brik på det samme felt. Felterne antages at være så store at en brik aldrig står i vejen for andre brikker.
Det er spillerens mål at samle alle brikker på samme felt –
med færrest mulige træk.
Ud over ovenstående regler for flytninger af en brik gælder følgende særlige
regel: Nårsomhelst kongen og en eller
flere riddere befinder sig på samme felt, kan spilleren vælge herefter at flytte kongen sammen med én af ridderne lige indtil
alle brikker er samlet. En flytning af
kongen sammen med en ridder tæller som ét træk og foregår efter reglen for
flytning af riddere.
Opgave
Skriv et program som finder det mindst mulige antal træk som er nødvendigt for at samle brikkerne.
Input data
Filen CAMELOT.IN indeholder brættets begyndelsestilstand, skrevet som en tegnstreng. Strengen indeholder en sekvens af op til 64 indbyrdes forskellige positioner på brættet. Den første er kongens position, de følgende er riddernes. Hver position er et par bestående af et bogstav og et ciffer. Bogstavet angiver den vandrette position, cifferet den lodrette (som vist i figur 1).
Eksempel på input
Kongen starter på feltet D4. Der er fire riddere, placeret på felterne A3, A8, H1 og H8.
Output data
Filen CAMELOT.OUT skal bestå af en enkelt linje med et heltal, nemlig det mindst mulige antal træk som er nødvendigt for at samle brikkerne.
Eksempel på output
Begrænsninger
0 £ antal riddere £ 63